Zdając sobie sprawę z faktu, że stosowanie symboli jest jedną z płaszczyzn aktywności matematycznej ucznia, ciągle poszukuję ulepszeń w sposobach wyrażania i zapisywania myśli matematycznej. I tak np. proponuję, aby fakty odkryte na lekcjach dotyczących przekształcenia wykresów funkcji były na koniec ujęte następującymi symbolami, zgodnie z regułą postępowania:

Tak wprowadzona symbolika pozwala uniknąć czasochłonnych opisów i jednocześnie jasno i precyzyjnie opisuje wykonywane czynności prowadzące do otrzymania wykresów funkcji złożonych np.:
![]()
W kwestii dotyczącej rozwiązywania zadań, zgodnie z tendencjami współczesnej dydaktyki stosuję podział na: ćwiczenia , zadania i problemy. Zaobserwowałam, że użycie słowa problem aktywizuje znacznie uczniów a i zeszyt lepiej wygląda od zeszytu, w którym są tradycyjne „zad.’’ I tak np. rutynowe zadanie:
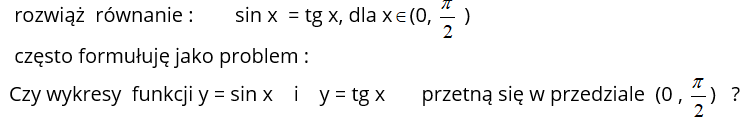
Uczniowie na ogół odpowiada początkowo twierdząco na to pytanie, ponieważ „widzą to z rysunku” , lecz po wykonaniu rachunków muszą zmienić zdanie. Zadanie to rozwijam, pytając następnie o wszystkie związania tego równania. Uczniowie wyciągają wniosek, że tangensoida przecina się z sinusoidą tylko w punktach o odciętych, będących całkowitymi wielokrotnościami liczby .
Uczniowie na ogół nie chcą być świadkami „wyreżyserowanych lekcji” i przyjmować jedynie gotowej wiedzy i gotowych przepisów na rozwiązywane problemy. Kiedyś na lekcji przytrafiła mi się następująca sytuacja: Uczniowi, wezwanemu do rozwiązania równania kwadratowego: x2-2001x + 2000 = 0 , mającemu problemy rachunkowe z tym rozwiązaniem, zaproponowałam, aby po prostu odgadł te rozwiązania, stosując wzory Viete’a .Uczeń rozumował tak: skoro iloczyn pierwiastków jest równy 2000, zaś suma 2001, to taki warunek spełniają liczby naturalne 1 i 2000 i sprawdzę:
12 – 2001 + 2000 = 0
oraz : 20002 - 2001· 2001 + 2000 = 2000 ( 2000 – 2001 ) + 2000 = - 2000 + 2000 = 0
Przedstawione rozwiązanie , z powodu jego „nieschematyczności”, inny z uczniów określił jako „niematematyczne” . Mieliśmy zatem okazję podyskutować i wyciągnąć wnioski.