Zaobserwowałam , że uczniowie lubią poznawać schematy ułatwiające im rachunki.
Warto tu wspomnieć o schemacie Hornera , który wprowadzam w celu nauczenia młodzieży dość sprawnego obliczania wartości wielomianów.
Schemat Hornera wprowadzam w następujący sposób :
Rozpatrzmy wielomian W(x) = anxn + an-1xn-1 + ......+ a1x + a0 , an
i utwórzmy następującą tabelkę : *

Oraz wypełnijmy ją według reguły:
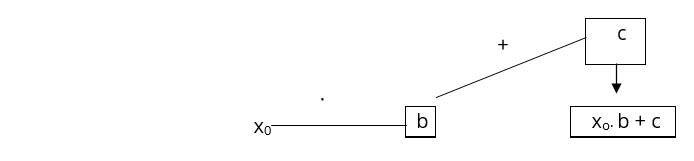
Następnie objaśniam jak według tej reguły obliczamy wartość wielomianu np. :
W (x) = 4x5 – 12 x4 + 5 x3 – 40 x – 15 , dla argumentu x = 3
Wtedy :
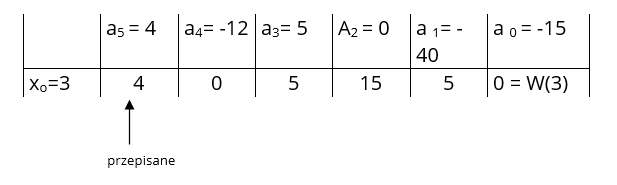
W słabszej klasie nie ma sensu uzupełnianie poniższej tabelki, lecz można wypełnić ją jedynie dla funkcji liniowej, kwadratowej oraz wielomianu stopnia 3.
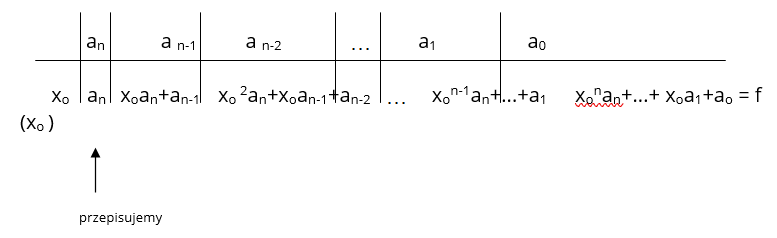
a ) dla funkcji liniowej f (x ) = ax + b :

b ) dla funkcji kwadratowej f (x) = ax2 + bx + c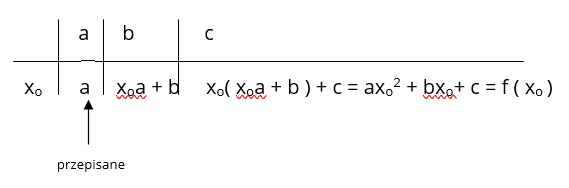
Na koniec pytanie: Czy jest sens wprowadzania tego schematu? Po kilkunastu latach praktyki szkolnej stwierdzam, że tak. Uczniowie szybko go opanowują i często go stosują. Okazuje się ,że najlepszy rachmistrz z klasy wolniej oblicza wartość wyrażenia :
4·35-12·34+5·33-40·3-15 niż przeciętny uczeń wykonujący to zadanie za pomocą schematu Hornera.