Jak zachęcać uczniów liceum do twórczego uczenia się matematyki? – Strona 5

Współczesna dydaktyka matematyki podkreśla korzyści z aktywnego udziału uczniów w procesie definiowania pojęć. Zwraca się uwagę na fakt , że „ ...dla wielu przeciętnych uczniów definicje i twierdzenia matematyczne pozostają martwe właśnie dlatego, że w procesie nauczania nie uwzględnia się wyraźnie, stale, konsekwentnie świadomie ze strony nauczyciela, tego istotnego ogniwa, jakim jest przekład definicji czy twierdzenia na jego operatywne , czynnościowe ujęcie...” Zofia Krygowska ,,Operatywny charakter matematyki i czynnościowe jej nauczanie”. Zarys dydaktyki matematyki, część I, WsiP,Warszawa,1977r.

Pokażę na przykładzie jak definiujemy liczby trójkątne :

Najpierw sporządzam poglądowy rysunek, obrazujący powstawanie kolejnych liczb trójkątnych:

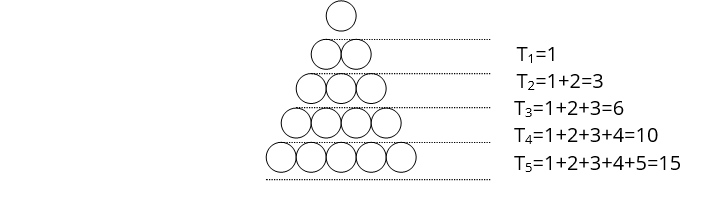
Po tak przeprowadzonej obserwacji , uczniowie samodzielnie definiują ciąg ( T_n) liczb trójkątnych sposobem rekurencyjnym.

DEFINICJA I : Ciąg liczb trójkątnych (T_n) opisany jest wzorem rekurencyjnym :

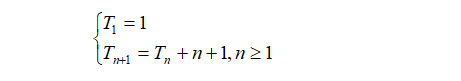
Stąd uczniowie formułują hipotezę : T_n = 1 + 2 + 3 +...+ n, co prowadzi do czynnościowego ujęcia definicji liczb trójkątnych:

DEFINICJA II : Jeśli dodam do siebie n początkowych dodatnich liczb naturalnych to otrzymam n-tą liczbę trójkątną.

Ci uczniowie, którzy pamiętają wzór *, udowadniany na pierwszej lekcji dotyczącej indukcji matematycznej

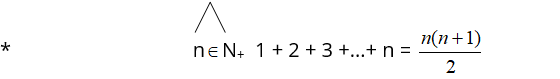
są w stanie utworzyć trzecią definicję liczb trójkątnych :

DEFINICJA III : Ciąg ( T_n ) liczb trójkątnych jest ciągiem o wyrazie ogólnym T_{n = .}

Chociaż liczby trójkątne nie są ujęte programem nauczania, nie zaszkodzi, aby w klasie z rozszerzonym programem matematyki wprowadzić ich różne definicje, a na kółku rozwinąć temat i zająć się np. liczbami piramidalnymi – wdzięcznym tematem niektórych konkursów matematycznych. Bardziej zainteresowanym matematyką uczniom warto postawić następujący problem: Znajdź wzór określający n-tą liczbę piramidalną P_n, wiedząc, że P_n=T₁+T₂+T₃+...+T_n .

Najistotniejszym mechanizmem aktywnego uczenia się matematyki jest rozwiązywanie zadań , na czym głównie oparte jest uczenie się matematyki.

Z punktu widzenia dydaktyki matematyki, pożądane byłoby rozwiązywanie tego samego problemu różnymi metodami i tzw. „ eksploatowanie” zadań do końca, wyciąganie wniosków służących rozwiązywaniu podobnych problemów, uogólnianie rozwiązań , a nawet jeśli się da – wypracowywanie przy czynnym zaangażowaniu uczniów, pewnych schematów na bazie rozwiązywanych problemów.

Strony: 123456789