Poniżej przedstawię jak rozwiązywałam z uczniami pewne zadanie dotyczące funkcji kwadratowej.
Zadanie: Dla jakich wartości parametru równanie (*) (m+1)x2-2x+m-1=0
ma dwa różne pierwiastki należące do przedziału (0,2) ?
I sposób:
Warunki zadania są spełnione dla tych m, dla których:
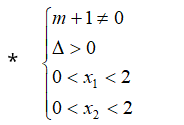
A zatem:
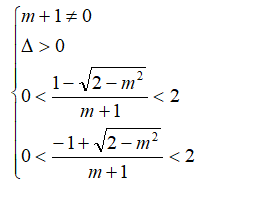
Ponieważ rozwiązanie nierówności podwójnych, w tym pierwiastkowych zajęłoby sporo czasu , myślimy nad innym sposobem rozwiązania tego zadania :
II sposób :
Układ * zapisujemy następująco:
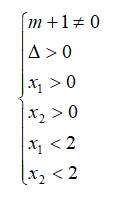

Dalej pozostaje jedynie zastosować wzory Viete’a.
III sposób rozwiązania tego zadania ( metodą graficzną ) opiera się na pewnym twierdzeniu dotyczącym funkcji kwadratowej :
Twierdzenie : Jeśli funkcja kwadratowa określona wzorem f(x) = ax2+bx+c ma dwa różne miejsca zerowe, to należą one do przedziału ( m , n ) wtedy i tylko wtedy, gdy
spełnione są warunki : a· f(m) > 0 i a· f(n) > 0 i ( m , n ).
(twierdzenie to było tematem zadania na ocenę celującą na egzaminie maturalnym w Gdańsku w roku 1995 – licea zawodowe i szkoły równorzędne )
Dowód implikacji „=>”
Założenia : Funkcja kwadratowa f(x) = ax2 + bx + c ma dwa różne miejsca zerowe
x1 , x2 ( m , n )
Teza : Spełnione są warunki : a·f(m) > 0 i a·f (n) > 0 i .
W dowodzie posługujemy się metodą graficzną
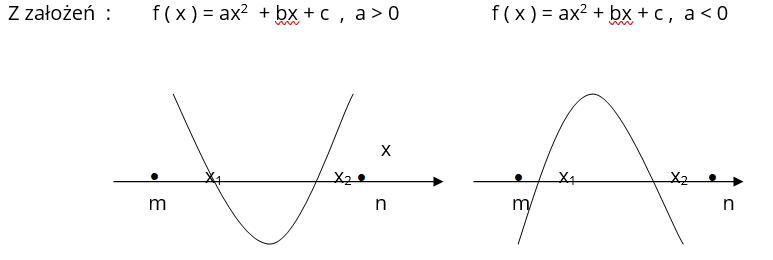
Z założeń mamy :
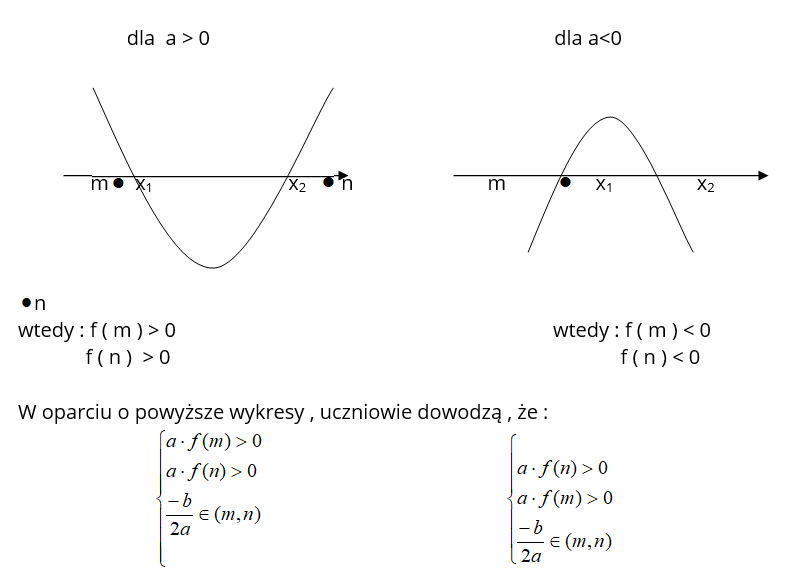
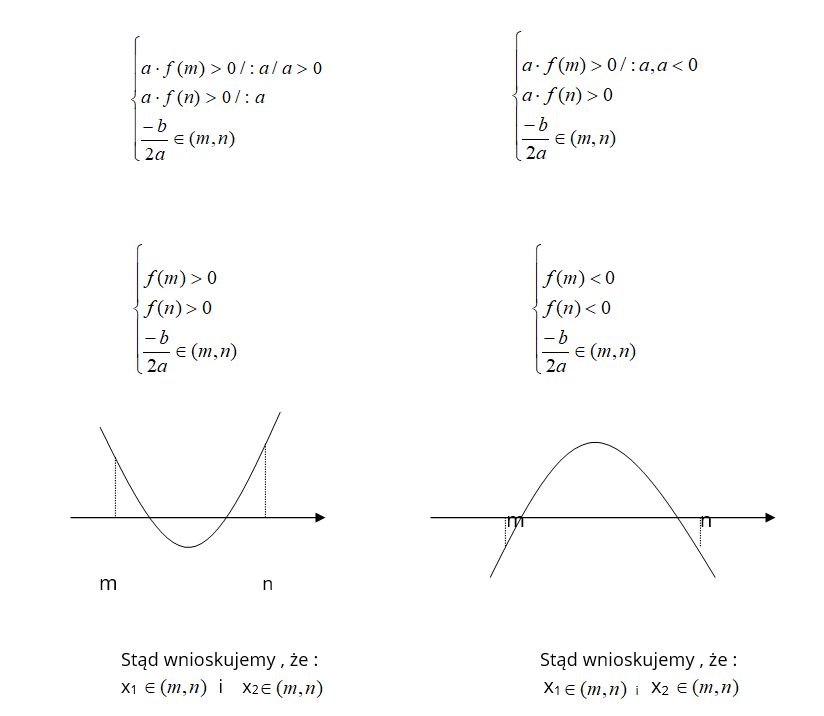
W oparciu o powyższe wykresy, uczniowie dowodzą, że:

Poprawne zapisanie do założeń i tezy , w celu udowodnienia implikacji „”sprawiało uczniom trochę kłopotu .
Założenia : Funkcja kwadratowa f ( x ) = ax2+ bx+c ma dwa różne miejsca zerowe x1 i x2 oraz spełnione są warunki :
a· f (m) > 0 i a·f ( n ) > 0 i -b/2a E (m,n).
Teza : x1 i x2 .
Dowód:

III sposób rozwiązania zadania
Pierwiastki równania ( m + 1 ) x2 – 2x + m – 1 = 0, należą do przedziału ( 0 , 2 ) dla tych m dla których spełniona jest alternatywa układów:
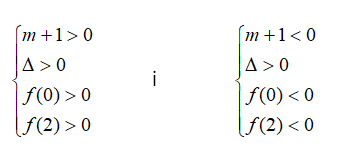
Powyższy sposób jest „ najłatwiejszy’’ rachunkowo.