Kończąc pracę, podsumowaliśmy i wyciągnęliśmy wnioski z naszego rozwiązania. W zbiorze zadań Dróbka I – II znalazłam zadanie, które łatwo rozwiązuje się I sposobem, bez odwoływania się do zbiorów Viete`a , oraz do metod graficznych. Jest to zadanie 7.90 :
Dla jakich wartości parametru m równanie: x2-2mx+m2-1=0 ma dwa rozwiązania należące przedziału <-2, 4>?
Udało mi się także , przy aktywności uczniów wypracować pewien schemat postępowania w przypadku sporej grupy zadań występujących kiedyś na maturze.
Zaczęło się od zadania 8.8, 4 ze strony 110 zbioru zadań z matematyki II klasy autorstwa Norberta Dróbki i Karola Szymańskiego.
Treść tego zadania brzmi : Wyznacz tak parametr a, aby układ :
a ) nie miał rozwiązania
b ) miał jedno rozwiązanie
c ) miał więcej niż jedno rozwiązanie

„ Na oko” nie widać , że to rozwiązanie jest błędne (****).
Aby sprowokować uczniów do dyskusji sugeruję , aby problemowi przyjrzeć się za pomocą metody graficznej . Proponuję rozpatrzyć układ dla a = 1 . Wtedy uczniowie widzą od razu , że parabola y = x2 – 1 przecina okrąg x2 + y2 = 1 w co najmniej trzech punktach :
( - 1 , 0 ) ; ( 1 , 0 ) ; ( 0 . – 1 ). A jeśli tak to wyżej podana odpowiedź jest błędna .
Wykonujemy rachunki :

Uczniowie zaobserwowali, że „x -ów „ jest więcej niż „y-ków” i że liczba „x-ów” decyduje o liczbie rozwiązań układu. Stąd następny wniosek, że przekształcenia powinny wyglądać tak:
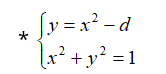
Podstawiając za y do drugiego równania po przekształceniach otrzymujemy równanie
** x4 + ( 1 – 2d) x2+ d2 – 1 = 0 i już wiedzą, że liczba rozwiązań układu *, zależy od liczby rozwiązań równania **. I tu pojawia się nowy problem: dyskusja liczby rozwiązań równania dwukwadratowego w zależności od parametru .
Wykonujemy podstawienie x2 = t i otrzymujemy równanie kwadratowe t2+( 1 – 2d)t + d2-1=0
Następnie kieruję do uczniów pytanie-wyzwanie: Wymyślcie jakiś sposób na to, żeby więcej nie błądzić ..... . Ci bardziej myślący sugerują, aby zająć się równaniem kwadratowym i prześledzić, jaki wpływ maja jego rozwiązania na rozwiązania równania dwukwadratowego, z uwzględnieniem wykonanego podstawienia x2 = t .
Budujemy tabelę , którą wypełniamy zgodnie z zaznaczonym kierunkiem.
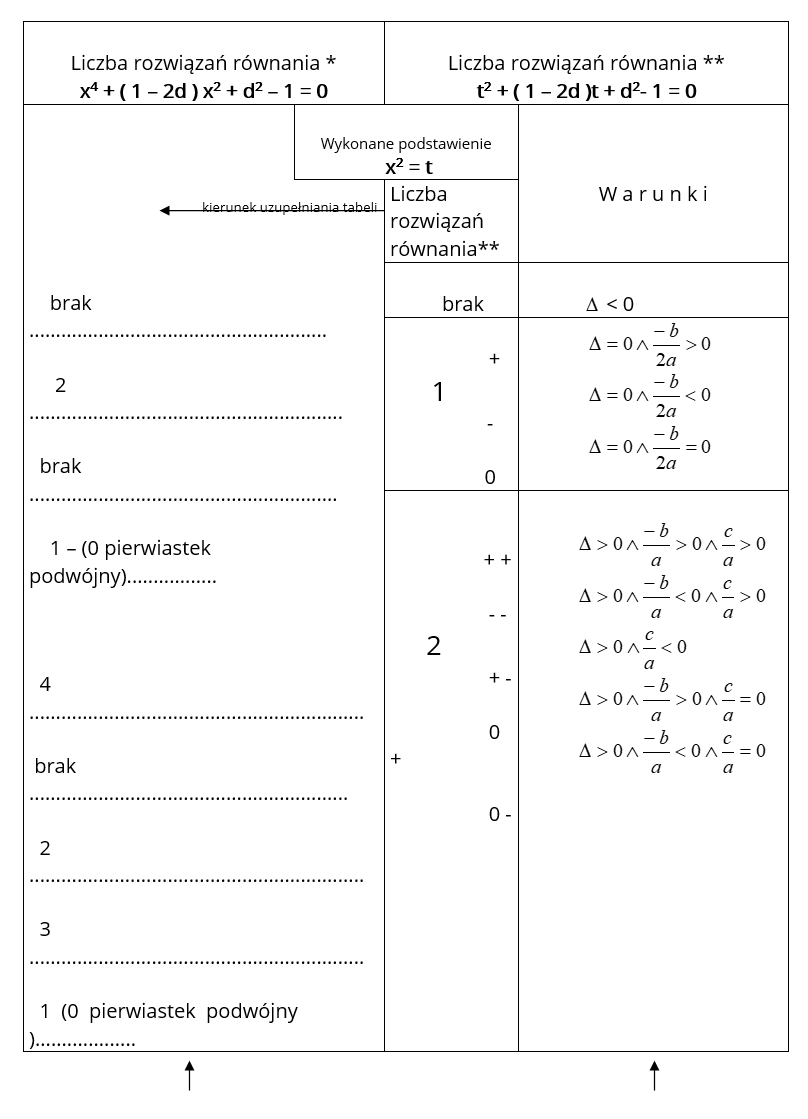
Pamiętamy o podstawieniu x2 = t.
Po tak schematycznym ujęciu, przedstawiamy następujące rozwiązanie :
I .Układ nie posiada rozwiązań dokładnie wtedy, gdy równanie * nie posiada rozwiązań,
a tak jest, gdy równanie ** :
1 ) nie posiada rozwiązań lub gdy
2 ) posiada dokładnie jedno rozwiązanie i nie jest nim liczba ujemna lub gdy
3 ) posiada dwa różne rozwiązania będące liczbami ujemnymi .
Układ nie posiada rozwiązań dla tych wartości parametru d, dla których spełniona jest alternatywa układów:
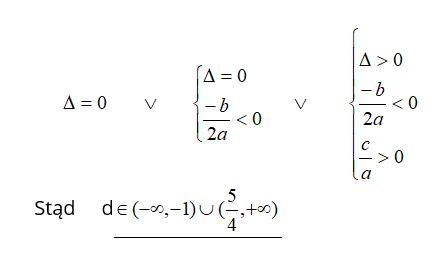
II Układ posiada jedno rozwiązanie wtedy, gdy równanie * posiada jedno rozwiązanie, a tak jest, gdy równanie ** :
1 ) posiada jedno rozwiązanie i jest nim zero lub gdy
2 ) posiada dwa różne rozwiązania jedno ujemne drugie równe zero.
Rozwiązując alternatywę , otrzymujemy:
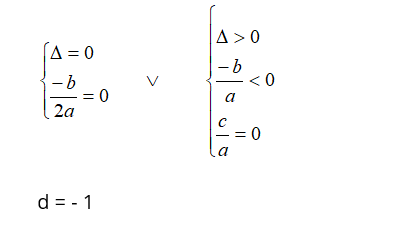
III . Układ posiada więcej niż jedno rozwiązanie wtedy, gdy równanie * posiada więcej niż
jedno rozwiązanie, a tak jest gdy równanie ** :
1 ) posiada jedno rozwiązanie i jest nim liczba dodatnia lub gdy
2 ) posiada dwa rozwiązania będące liczbami dodatnimi lub gdy
3 ) posiada dwa rozwiązania - jedno dodatnie drugie ujemne lub gdy
4 ) posiada dwa rozwiązania - jedno dodatnie drugie równe zero.
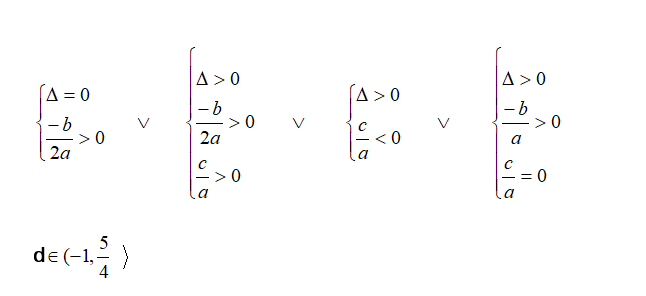
Dość sprawne rozwiązanie układu było spowodowane tym, że pod wykonaną tabelką rozwiązaliśmy pomocnicze nierówności i równania, otrzymując :
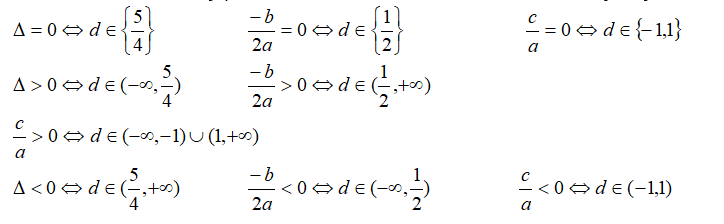
Po tak wykonanym przygotowaniu, rozwiązanie zadania prowadziło do poprawnego wyniku.